Vous ne pouvez pas vous être intéressé à l’investissement boursier sans jamais avoir entendu le mot « diversification » de la part d’un de vos interlocuteurs professionnels. D’où vient-elle ? A quoi sert-elle ?

Quelle est l’origine de la diversification financière ?

La diversification est devenue centrale dans la finance moderne depuis qu’Harry Markowitz a démontré mathématiquement sa pertinence dans la composition du portefeuille d’un investisseur.

Nous vous épargnons la démonstration mathématique de peur que vous ne lisiez pas la suite de cet article. Cependant, les fous de maths pourront trouver davantage d’information ici.

En finance, le risque d’un actif est caractérisé par la volatilité de cet actif. En gros, la volatilité est la moyenne des variations journalières du cours d’un actif sur une période donnée, par exemple 30 jours ou une année (c’est un peu plus compliqué que cela, mais c’est l’idée). Plus les variations journalières du prix d’un actif sont grandes, plus cet actif est volatil et plus il est considéré risqué. Par exemple, une valeur biotech est plus volatile qu’une société immobilière réglementée (SIR). Elle est donc plus risquée. En contrepartie, la plus-value espérée d’un investissement dans une biotech est bien supérieure à celle d’une SIR. Il n’y a pas de secret, pour espérer gagner plus, il faut prendre plus de risque.

Le rendement et le risque pour définir la frontière efficiente d’un portefeuille

En partant de ces deux concepts que sont le rendement espéré et le risque, défini comme la volatilité d’un actif, Harry Markowitz a théorisé, en 1952, la frontière efficiente d’un portefeuille dans le « Journal of Finance ». Derrière ce terme se cache la combinaison optimale d’actifs en fonction de deux paramètres, le rendement espéré et le risque toléré par un investisseur. Cette combinaison optimale varie donc d’un individu à l’autre.

Observons tout d’abord le risque. Comment évaluer celui d’un portefeuille qui comprend plusieurs titres ? On ne peut pas se contenter de calculer la moyenne des volatilités des titres qui composent ce portefeuille, car il faut également tenir compte de ce qu’on appelle la corrélation entre les actifs. La corrélation entre deux actifs mesure le degré de similitude des évolutions boursières de ces actifs. On dit que deux actifs ont une corrélation parfaite (100%) si leurs cours de bourse évoluent exactement de la même façon. Dans la pratique, cela n’existe pas. Mais on peut considérer qu’un portefeuille composé de deux positions identiques, i.e. dont la corrélation est parfaite, présente un risque équivalent à celui du titre détenu, une fois, deux fois, trois fois. Peu importe, en ajouter ou en retirer ne change rien à la volatilité du portefeuille. Jusque-là, La Palice n’aurait sans doute pas trouvé mieux.

Par contre, si deux actifs évoluent en sens parfaitement opposé, leur corrélation est de -100%. Combiner dans un portefeuille deux actifs dont la corrélation est -100% annule le risque de ce portefeuille, quel que soit le niveau de risque (i.e. de volatilité) de chaque actif. Si j’achète 100 actions Cofinimmo et que je vends à terme les mêmes 100 actions Cofinimmo, je ne supporte plus aucun risque. Vous me direz que je n’y gagne rien non plus. Certes, mais sans risque, pas de rendement. Ce sont ici des cas extrêmes. Les actifs ne sont jamais parfaitement corrélés ou décorrélés.

L’idée à retenir est double :

• Les actifs présentant des corrélations non parfaites (i.e. inférieures à 100%), ajouter un actif dans un portefeuille, sous réserve du bon dosage, en fait baisser le risque ;
• Plus la corrélation est faible entre les actifs, plus le risque du portefeuille se réduit.

En ce qui concerne le rendement escompté d’un portefeuille, son évaluation est plus facile. Il suffit de calculer la moyenne pondérée du rendement escompté de chaque actif par le poids de celui-ci. Par contre, il est moins trivial d’évaluer le rendement escompté d’un actif en particulier. Un moyen simple est de se référer aux prévisions moyennes des analystes.

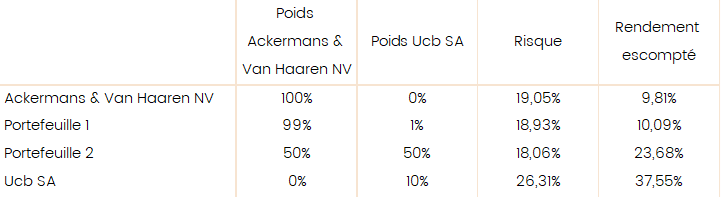
Petite illustration avec les deux valeurs Ackermans & van Haaren et UCB (voir tableau ci-dessous). UCB est plus risquée qu’Ackermans & van Haaren, mais son potentiel de gain est très supérieur. La corrélation entre les deux valeurs s’élève à 22%. Grâce à elle, ajouter 1% d’UCB à un portefeuille d’Ackermans augmente le rendement escompté sans augmenter le risque. Vous avez compris l’idée.

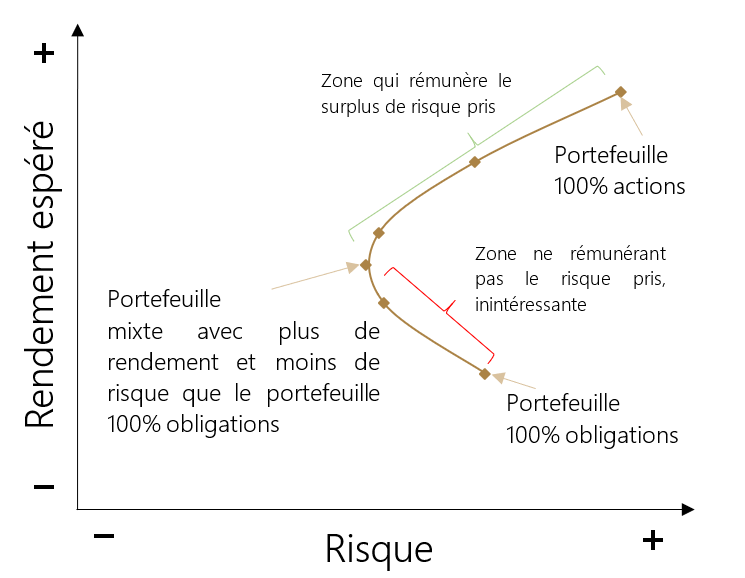
Ce raisonnement fonctionne également pour les classes d’actifs entre elles. Selon les mêmes principes, un portefeuille composé uniquement d’obligations, aussi diversifié soit-il, sera toujours plus risqué que le même portefeuille auquel on aurait ajouté ne fût-ce qu’1% d’actions, compte tenu de la corrélation imparfaite (< 100%) entre ces deux classes d’actifs. Le graphique ci-dessous illustre ce principe.

Les limites de la théorie moderne du portefeuille d’Harry Markowitz

Soyons clairs, en théorie tout est merveilleux. En pratique, les choses sont moins évidentes. Le modèle présente plusieurs limites :

• Il considère que l’investisseur est rationnel et ne réagit pas selon ses émotions. Or nous avons vu (voir la rubrique « Quand la psychologie rencontre la finance ») que nos biais comportementaux (e.g. l’excès de confiance) pouvaient altérer notre rationalité ;
• La volatilité est établie sur des données historiques. Or rien ne garantit qu’elle se comportera de la même manière dans le futur ;
• Les rendements sont estimés sur la base de différents scénarios. Ici aussi, rien ne garantit que ces scénarios seront les bons.

Malgré ces limites, il est irréfutable que la diversification est indispensable pour tout portefeuille.

La diversification est le seul repas gratuit. Harry Markowtiz.

Retenez donc :

• Peu importe la classe d’actif, détenir un seul actif en portefeuille sera toujours plus risqué qu’en détenir au moins deux ;
• Un portefeuille composé à 100% d’obligations est plus risqué et offre moins de rendement qu’un portefeuille mixte défensif. En d’autres termes, consacrer une petite partie de son portefeuille obligataire aux actions diminue le risque global et augmente l’espérance de rendement.

Voilà, vous savez l’essentiel de l’origine de la diversification et de ses effets sur un portefeuille.